This blog is the second part of our series, where we share the Python code used in our paper titled: Bayesian Analysis of Fracture of Polyamide 12 U-Notched Specimens, developed in collaboration with the research group of Professor Jesús Rodríguez-Pérez (DIMME, Grupo de Durabilidad e Integridad Mecánica de Materiales Estructurales, Escuela Superior de Ciencias Experimentales y Tecnología, Universidad Rey Juan Carlos). The paper was presented at the European Conference of Fracture 2024
The objective is to apply a methodology for selecting the most suitable failure criteria to predict the maximum load of notched Polyamide 12 solids.
We describe step by step the code used
import autograd.numpy as np import pymc3 as pm import matplotlib.pyplot as plt import arviz as az
In U-notched solids, the stress field near the notch tip can be estimated using the Creager and Paris formula. The approximated stress field depends on the notch radius and the notch stress intensity factor, KU. For two geometries with the same radius, the failure of the component initiates when this factor reaches a critical value, KUC , which is a function of the nothc tip rdius. Fracture can be formulated knowing the generalized toughness funcion KUC.
This material function can be obtained experimentally by performing a fracture test for each value of the notch radius, or by assuming a failure criteria and applying it. (See Gómez, F.J., Guinea, G.V., Elices, M., 2006. Failure criteria for linear elastic materials with U-notches. International Journal of Fracture 141(1–2). doi: 10.1007/s10704-006-0066-7.)
In the current research, six failure criteria are compared and studied.
- Theory of critical distance 1 (TCD- 1) – Mean stress criterion
- Theory of critical distance 2 (TCD- 2) – Maximum stress criterion
- CSED: Mean strain energy density criterion
- FFM: Finite fracture mechanics
- CSZ-L: Cohesive Zone Model with linear softening curve
- Phen: Phenomenological formulation
All failure criteria are formulated using two parameters, the material fracture toughness and the fracture stress.
pi = np.pi
def KN_func1(KIC,ft, R):
# T(t)
L = (KIC/ft)**2*1000
KN = KIC*(1+pi*R/L)**1.5/(1+2*pi*R/L)
return KN
def KN_func2(KIC,ft, R):
# T(t)
L = (KIC/ft)**2*1000
KN = KIC*(1+pi*R/(4*L))**0.5
return KN
def KN_func3b(KIC,ft, R):
L = (KIC/ft)**2*1000
m1 = 81.352
m2=408.31
m3=585.77
m4=83.052
m5=622.39
KN = KIC*((1+m1*(R/L)+m2*(R/L)**2+m3*(R/L)**3+pi/4*(R/L)**4)/(1+(R/L)**3+m4*(R/L)+m5*(R/L)**2 ))**0.5
return KN
def KN_func4(KIC,ft, R):
# T(t)
L = (KIC/ft)**2*1000
KN = KIC*0.947/(1-1/2.284*R/L*np.log(1+2.284*L/R))**0.5
return KN
def KN_func5(KIC,ft, R):
# T(t)
L = (KIC/ft)**2*1000
KN = KIC*(1+pi*R/(4*L)+(-0.79835*R/L-2.1658*(R/L)**2+19.501*(R/L)**3-48.167*(R/L)**4)/(1+117.31*(R/L)**4))**0.5
return KN
def KN_func6(KIC,ft, R):
# T(t)
L = (KIC/ft)**2*1000
KN = KIC*((1+0.47392*(R/L)+2.1382*(R/L)**2+pi/4*(R/L)**3)/(1+(R/L)**2 ))**0.5
return KN
failure_criteria = {
'TCD 1' : KN_func1,
'TCD 2' : KN_func2,
'CSED' : KN_func3b,
'FFM' : KN_func4,
'CZM - L' : KN_func5,
'Phen.' : KN_func6
}
# Set fixed parameters for synthetic data
KIC = 3.25
ft = 82.0
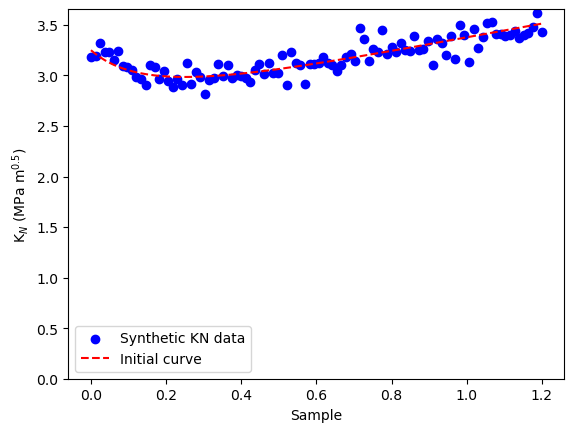
# Generate synthetic data
N = 100 # Number of data points
radio_vect = np.linspace(1e-5, 1.2, N)
mean_KN = KN_func1(KIC,ft, radio_vect)
# Adding noise to simulate real measurements
kn_vect = mean_KN + np.random.normal(0, 0.1,N)
# Plot the synthetic data
plt.scatter(radio_vect, kn_vect, color='blue', label='Synthetic KN data')
plt.plot(radio_vect,mean_KN, color='red', linestyle='--', label='Initial curve')
plt.xlabel('Sample')
plt.ylabel(r'K$_N$ (MPa m$^{0.5}$)')
plt.ylim([0,None])
plt.legend()
plt.show()
data = {
'radio_vect': radio_vect,
'kn_vect': kn_vect
}
- KIC: Represents the critical stress intensity factor (fracture toughness).
- ft: Critical stress.
- ϵ: The error parameter.
We’ll specify priors for the two material parameters, and, the standard deviation.
class BayesianModelFitter:
def __init__(self, data,kn_fun):
"""
Initialize the BayesianModelFitter with the necessary data.
Parameters:
- data: Dictionary or DataFrame containing the data needed for the model.
"""
self.data = data
self.kn_fun = kn_fun
self.trace = None
self.model = None
def fit_model(self):
"""Set up and fit the Bayesian model using PyMC3."""
with pm.Model() as self.model:
# Example model setup (adjust according to actual needs)
KIC = pm.Uniform('KIC', 1, 5) # Prior example
ft = pm.Uniform('ft', 10, 150)
ϵ = pm.InverseGamma('ϵ', alpha=1.0,beta=1)
radio_vect = self.data['radio_vect']
kn_vect = self.data['kn_vect']
KN_pred = pm.Normal('KN_pred', mu=self.kn_fun(KIC,ft, radio_vect), sd=ϵ, observed=kn_vect)
self.trace = pm.sample(3000, tune=1000,cores=3)
return self.trace
def plot_posterior(self):
"""Plot the fitting results using Arviz."""
if self.trace:
az.plot_trace(self.trace)
plt.show()
else:
print("Model has not been fitted yet. Please run fit_model() first.")
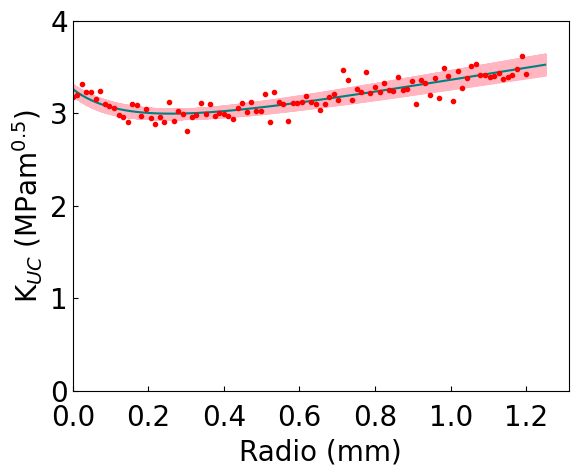
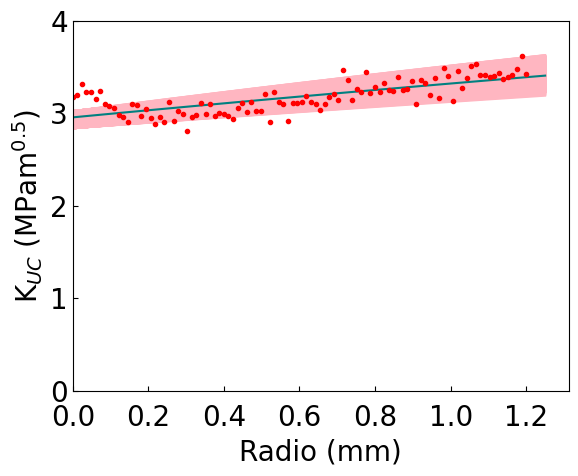
def plot_fit(self):
"""Plot the fitting results using Arviz."""
if self.trace:
xr = np.linspace(0,1.25,100)
KIC_m = self.trace['KIC'].mean()
ft_m = self.trace['ft'].mean()
draws = range(0,len(self.trace['KIC']),25)
az.style.use("default")
fig,ax = plt.subplots()
for i in draws:
for j in draws:
plt.plot(xr,self.kn_fun(self.trace['KIC'][i],self.trace['ft'][j],xr),c='lightpink')
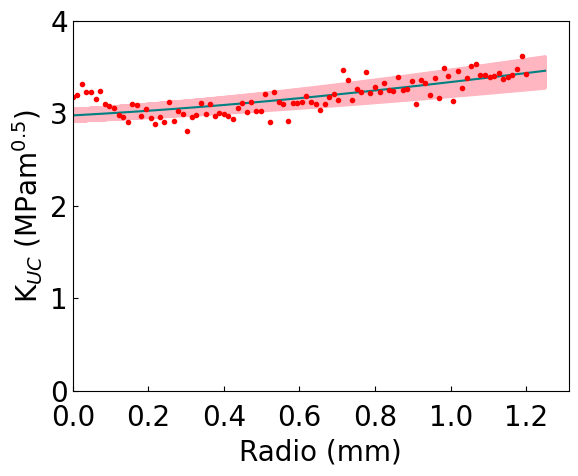
ax.plot(xr,self.kn_fun(KIC_m,ft_m, xr),c='teal')
ax.plot(radio_vect,kn_vect,'C0.',color='red')
ax.set_xlim(0,None)
ax.set_ylim(0,4)
ax.tick_params(axis="y",direction="in")
ax.tick_params(axis="x",direction="in",pad=10)
plt.ylabel(r'K$_{UC}$ (MPam$^{0.5}$)',fontsize=20)
plt.xlabel('Radio (mm)',fontsize=20)
plt.yticks([0,1,2,3,4],fontsize=20)
plt.xticks(fontsize=20)
plt.show()
else:
print("Model has not been fitted yet. Please run fit_model() first.")
def calculate_waic(self):
"""Calculate and return the WAIC value of the fitted model."""
if self.trace and self.model:
waic = az.waic(self.trace)
print(f"WAIC: {waic.waic}")
return waic.waic
else:
print("Model has not been fitted yet. Please run fit_model() first.")
return None
trace = dict()
waic = dict()
for key in failure_criteria.keys():
KN_func = failure_criteria[key]
fitter = BayesianModelFitter(data,KN_func)
trace_g = fitter.fit_model()
print(key)
fitter.plot_fit()
az.summary(trace_g)
trace[key] = trace_g
waic[key] = fitter.calculate_waic()
TCD 1
TCD 2
CSED
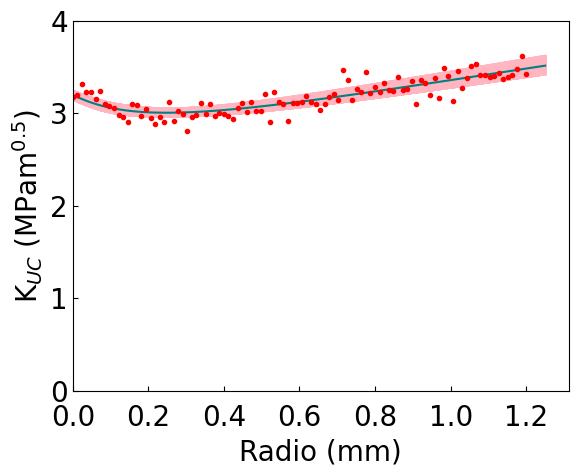
FFEM
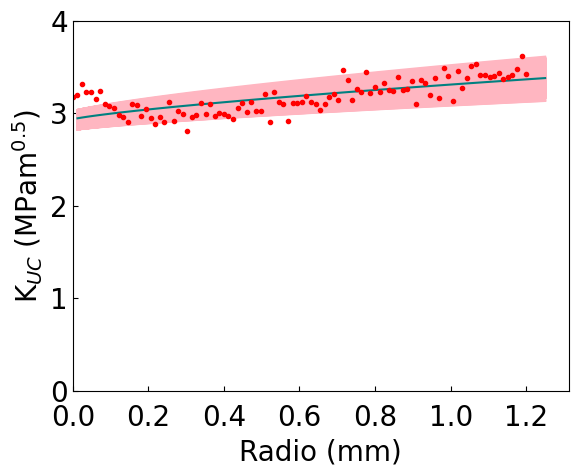
CZM-L
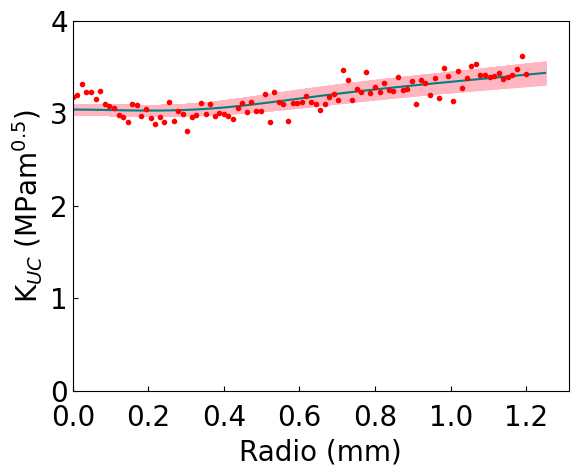
Phen.
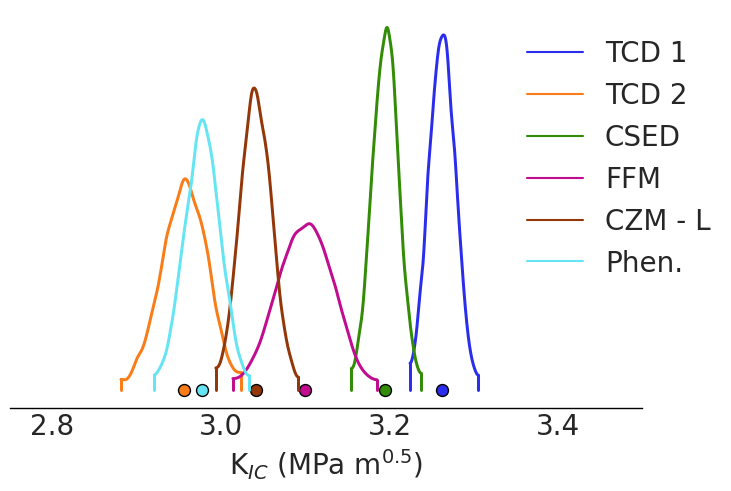
az.style.use("arviz-white")
datas = list(trace.values())
az.plot_density(datas,var_names=['KIC'],textsize=20,hdi_prob=0.99,data_labels=trace.keys())
#trace_fig.set_xticklabels(x_labels, fontsize=14)
plt.xlabel(r'K$_{IC}$ (MPa m$^{0.5}$)',fontsize=20)
plt.title('')
#plt.legend( loc='upper center',fontsize=20)
#plt.legend( loc=(0.7, 0.6),fontsize=20)
plt.legend( loc=(0.8, 0.3),fontsize=20)
plt.xlim(2.75,3.5)
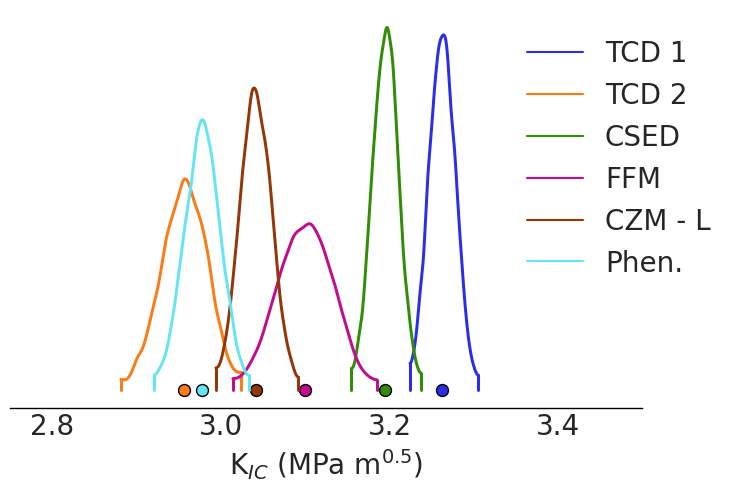
| Failure criteria | WAIC |
|---|---|
| TCD-1: Mean stress criterion | 95.57 |
| TCD-2: Maximum stress criterion | 63.82 |
| CSED: Mean strain energy density criterion | 93.93 |
| FFM: Finite fracture mechanics | 59.08 |
| CSZ-L: Cohesive Zone Model with linear softening curve | 80.28 |
| Phen: Phenomenological formulation | 70.75 |
Following the previous table two failure criteria are proposed: FFM – Finite fracture mechanics and TCD-2 – Maximum stress criterion.
