Numerical code corresponding to our publication titled: Bayesian analysis of fracture of polyamide 12 U-notched specimens. Part -1 Bayesian non-linear regression

Deja un comentario / Uncertainty assessment

Recently, we have presented a paper titled: Bayesian analysis of fracture of polyamide 12 U-notched specimens, in collaboration with the group of Professor Jesús Rodríguez-Pérez (DIMME, Grupo de Durabilidad e Integridad Mecánica de Materiales Estructurales, Escuela Superior de Ciencias Experimentales y Tecnología, Universidad Rey Juan Carlos) in the European Conference of Fracture 2024

We share the Python code in this blog using synthetic notched fracture data as an example of Bayesian non-linear regression.

We describe step by step the code used

Step 1: Import Libraries

Import the required libraries. In this blog, we are substituting PYMC3 by PYMC to facilitate and simplify the installation process.

import numpy as np
import matplotlib.pyplot as plt

import pymc as pm
import arviz as az

Step 2: Generate Synthetic Data

We’ll create a synthetic dataset following one of the failure criteria studied in our paper. Original data can be found in previous publications as: Crespo, M., Gómez-del Río, M.T., Rodríguez, J., 2017. Failure of SLS polyamide 12 notched samples at high loading rates. Theoretical and Applied Fracture Mechanics 92. doi: 10.1016/j.tafmec.2017.08.008.
Crespo, M., Gómez-del Río, T., Rodríguez, J., 2019. Failure of polyamide 12 notched samples manufactured by selective laser sintering. Journal of Strain Analysis for Engineering Design 54(3). doi: 10.1177/0309324719847817. 

def KN_func(KIC, ft, R):
    pi = np.pi
    L = (KIC / ft) ** 2 * 1000
    KN = KIC * (1 + pi * R / L) ** 1.5 / (1 + 2 * pi * R / L)
    return KN

# Fixed parameters for synthetic data
KIC = 3.25  
ft = 82.0    

# Generate synthetic data
N = 100  # Number of data points
radio_vect = np.linspace(0, 1.2, N)
mean_KN = KN_func(KIC,ft, radio_vect)

# Adding noise to simulate real measurements
observed_KN_values = mean_KN + np.random.normal(0, 0.3,N)

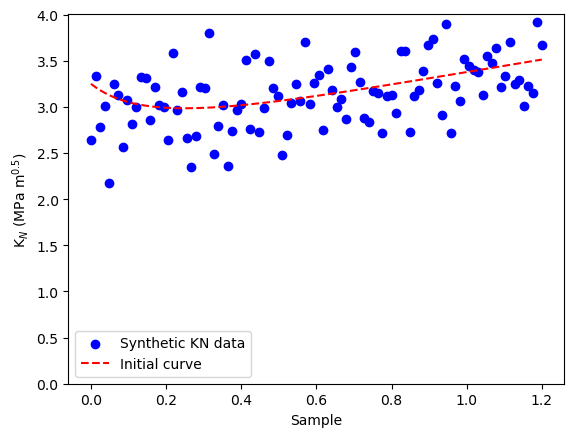
# Plot the synthetic data
plt.scatter(radio_vect, observed_KN_values, color='blue', label='Synthetic KN data')
plt.plot(radio_vect,mean_KN, color='red', linestyle='--', label='True KN curve')
plt.xlabel('Sample')
plt.ylabel(r'K$_N$ (MPa m$^{0.5}$)')
plt.ylim([0,None])
plt.legend()
plt.show()

Step 4: Define the Bayesian Model

Now, we’ll set up the Bayesian model using PyMC. The local failure criterion proposed has two parameters, the fracture toughness and the critical stress. It is assumed that the experimental error does not depend on the notch radius.

  • KIC​: Represents the critical stress intensity factor (fracture toughness).
  • ft​: Critical stress.
  • ϵ: The error parameter.

We’ll specify priors for the two material parameters, and, the standard deviation.

with pm.Model() as model:
    # Priors for KIC, ft, and R based on domain knowledge
    KIC = pm.Uniform('KIC', 1, 5)
    ft = pm.Uniform('ft', 10, 150)
    ϵ = pm.InverseGamma('ϵ', alpha=1.0,beta=1)

    # Likelihood: observed data is compared against the model function
    KN_observed = pm.Normal('KN_observed', mu=KN_func(KIC, ft, radio_vect), sigma=ϵ, observed=observed_KN_values)

    # Inference
    trace = pm.sample(2000, tune=1000, return_inferencedata=True,cores=3)

Step 5: Analyze the Results

After running the Bayesian inference, the posterior distribution for the material parameters can be plotted.

Using arviz, a powerful library for Bayesian analysis, we plot the trace of the parameters and their posterior distributions:

trace_fig = az.plot_trace(trace, var_names=[ 'KIC', 'ft','ϵ'], figsize=(12, 15));

# get and change x labels
for i in range(trace_fig.shape[0]):
    for j in range(trace_fig.shape[1]):
        if j==0:
            x_labels = [str(np.round(x,3)) for x in trace_fig[i][j].get_xticks()];
            trace_fig[i][j].set_xticklabels(x_labels, fontsize=14);     
            
        if j==1:
            y_labels = [str(np.round(y,3)) for y in trace_fig[i][j].get_yticks()];
            trace_fig[i][j].set_yticklabels(y_labels, fontsize=14);
            
            x_labels = [str(int(x)) for x in trace_fig[i][j].get_xticks()];
            trace_fig[i][j].set_xticklabels(x_labels, fontsize=14);
            
        title=trace_fig[i][j].get_title()
        trace_fig[i][j].set_title(title, fontsize=20);
        
trace_fig[0][0].set_title(r'K$_{IC}$',  fontsize=20);
trace_fig[0][1].set_title(r'K$_{IC}$',  fontsize=20);

trace_fig[1][0].set_title(r'$f_{t}$',  fontsize=20);
trace_fig[1][1].set_title(r'$f_{t}$',  fontsize=20);

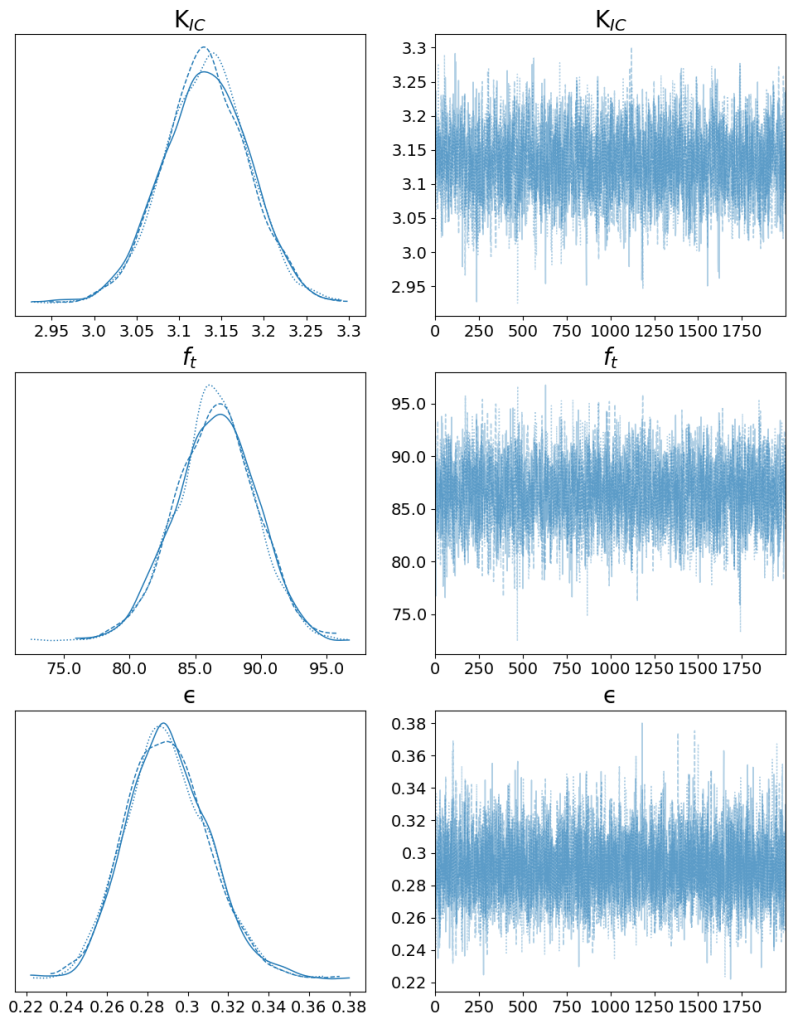
The posterior distribution can be plotted in better quality

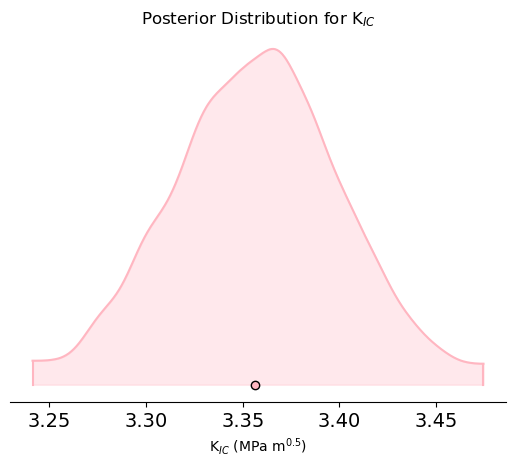
# Plot the posterior distribution for KIC

az.plot_density(trace, var_names=['KIC'], shade=0.3, hdi_prob=0.99,colors='lightpink')
plt.xlabel(r'K$_{IC}$ (MPa m$^{0.5}$)')
plt.title('Posterior Distribution for K$_{IC}$')
plt.show()

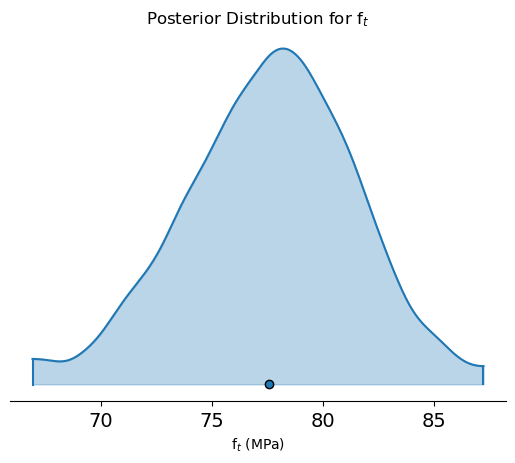
az.plot_density(trace, var_names=['ft'], shade=0.3, hdi_prob=0.99)
plt.xlabel(r'f$_{t}$ (MPa)')
plt.title('Posterior Distribution for f$_{t}$')
plt.show()

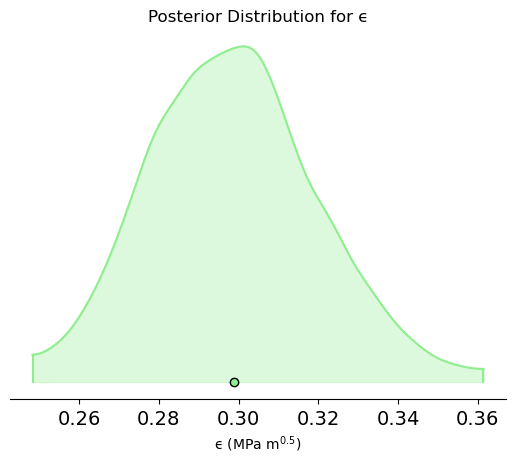
az.plot_density(trace, var_names=['ϵ'], shade=0.3, hdi_prob=0.99,colors='lightgreen')
plt.xlabel(r'ϵ (MPa m$^{0.5}$)')
plt.title('Posterior Distribution for ϵ')
plt.show()

# Summarize the results
summary = az.summary(trace)
print(summary)

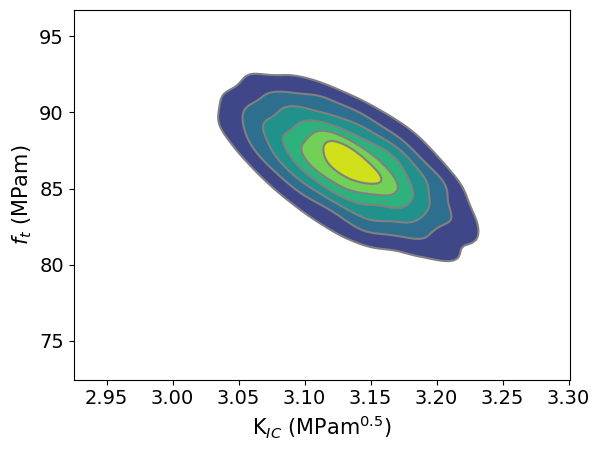
The parameter region that fits the experimental results can be studied with the next code

az.plot_pair(trace,kind='kde', var_names=[ 'KIC', 'ft'])
plt.ylabel(r'$\sigma_{C}$ (MPam)')
plt.xlabel(r'K$_{IC}$ (MPam$^{0.5}$)')

Step 6: Plot the Final Fitting

Now, let’s visualize the Bayesian fitting results by plotting the final regression .

# Posterior samples
posterior_KIC = trace.posterior['KIC'].values.flatten()
posterior_ft = trace.posterior['ft'].values.flatten()

KICmean = trace.posterior['KIC'].mean().values
ftmean = trace.posterior['ft'].mean().values
fit_KN = KN_func(KICmean,ftmean, radio_vect)

# Select some posterior samples for plotting
num_samples = 500  # Number of samples to plot
posterior_samples_idx = np.random.choice(len(posterior_KIC), num_samples, replace=False)

# Plot original data vs. posterior curves
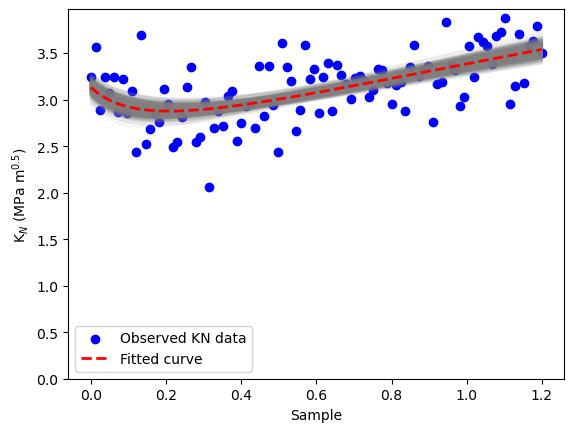
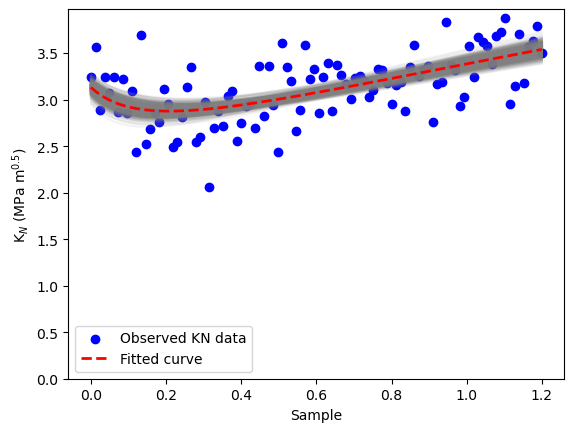
plt.scatter(radio_vect, observed_KN_values, color='blue', label='Observed KN data')
for i in posterior_samples_idx:
    plt.plot(radio_vect, KN_func(posterior_KIC[i], posterior_ft[i], radio_vect), color='gray', alpha=0.1)

# Plot the true KN curve
plt.plot(radio_vect, fit_KN, 'r--', label='Fitted curve', linewidth=2)
plt.xlabel('Sample')
plt.ylabel(r'K$_N$ (MPa m$^{0.5}$)')
plt.ylim([0,None])
plt.legend()
plt.show()

Conclusions

In this blog, we have successfully applied Bayesian inference to estimate the fracture toughness from notched specimens. By using probabilistic programming techniques, we were able to quantify the uncertainty in our parameter estimates and provide meaningful insights into the material behavior.
The step-by-step approach outlined above can be applied to other engineering and material science problems where uncertainty and complex relationships between variables must be modeled.

Deja un comentario