Bayesian Fitting of Data from Three Groups with Parallel Linear Regression Lines

Deja un comentario / Uncertainty assessment

When fitting data distributed across multiple groups, Bayesian modeling offers a powerful approach to account for uncertainty in parameter estimation. In this blog, we’ll walk through how to fit data from three different groups where each group can be described by a linear regression model, and the three regression lines are parallel).

Step 1: Install Required Libraries

Install the necessary libraries

pip install pymc3 numpy matplotlib seaborn

Step 2: Import Libraries

Import the required libraries

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pymc3 as pm

Step 3: Generate Synthetic Data

We’ll create a synthetic dataset with three groups. Each group will have a different intercept, but the slope will be the same across all groups to ensure that the lines are parallel.

np.random.seed(42)

# Number of data points per group
n_points = 50

# Shared slope for all groups
true_slope = 2.0

# Different intercepts for each group
intercepts = [1.0, 3.0, 5.0]

# Generate synthetic data for three groups
X = np.linspace(0, 10, n_points)
Y = []
group_labels = []

for idx, intercept in enumerate(intercepts):
    # Generate linear data with some noise
    Y_group = true_slope * X + intercept + np.random.normal(0, 1, n_points)
    Y.append(Y_group)
    group_labels.extend([f'Group {idx+1}'] * n_points)

# Flatten the Y array and repeat X for all groups
Y = np.concatenate(Y)
X = np.tile(X, 3)

# Encode group labels as integers for modeling
group_idx = np.array([0] * n_points + [1] * n_points + [2] * n_points)

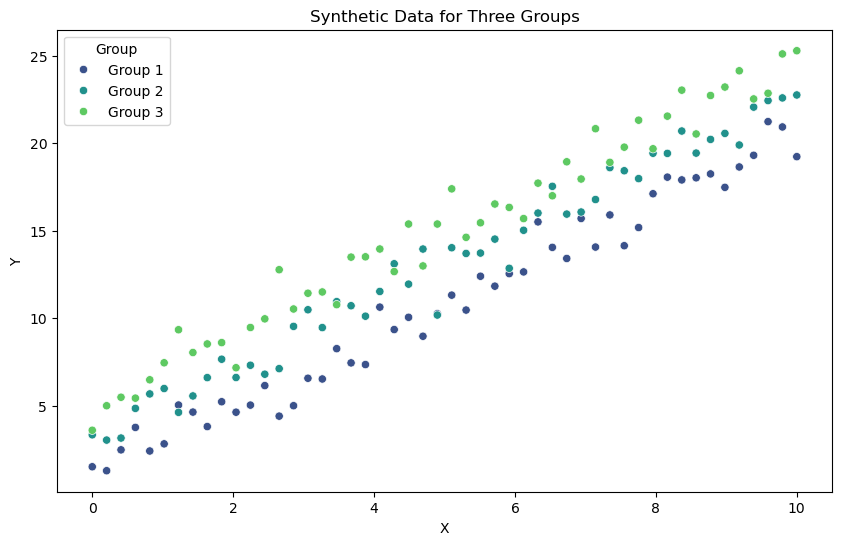
# Visualize the data
plt.figure(figsize=(10, 6))
sns.scatterplot(x=X, y=Y, hue=group_labels, palette='viridis')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Synthetic Data for Three Groups')
plt.legend(title='Group')
plt.show()

Step 4: Define the Bayesian Model

Now, we’ll set up the Bayesian model using PyMC3. We’ll specify priors for the shared slope and for the intercepts of each group. We’ll also define a prior for the standard deviation of the noise.

# Step 4: Define the Bayesian model
with pm.Model() as bayesian_model:
    # Shared slope for all groups
    slope = pm.Normal('slope', mu=0, sigma=10)
    
    # Intercepts for each group
    intercepts = pm.Normal('intercepts', mu=0, sigma=10, shape=3)
    
    # Noise standard deviation
    sigma = pm.HalfNormal('sigma', sigma=1)
    
    # Expected value of Y for each group
    # Use indexing to select the correct intercept for each data point based on its group
    mu = slope * X + intercepts[group_idx]
    
    # Likelihood (data generation process)
    Y_obs = pm.Normal('Y_obs', mu=mu, sigma=sigma, observed=Y)

    # Inference using Markov Chain Monte Carlo (MCMC)
    trace = pm.sample(1000, tune=1000, cores=2, target_accept=0.95)

Step 5: Analyze the Results

After running the Bayesian inference, we need to analyze the trace data to understand the posterior distributions of the model parameters (slope, intercepts, and noise standard deviation). We can use built-in functions in PyMC3 to summarize and plot the posterior distributions.

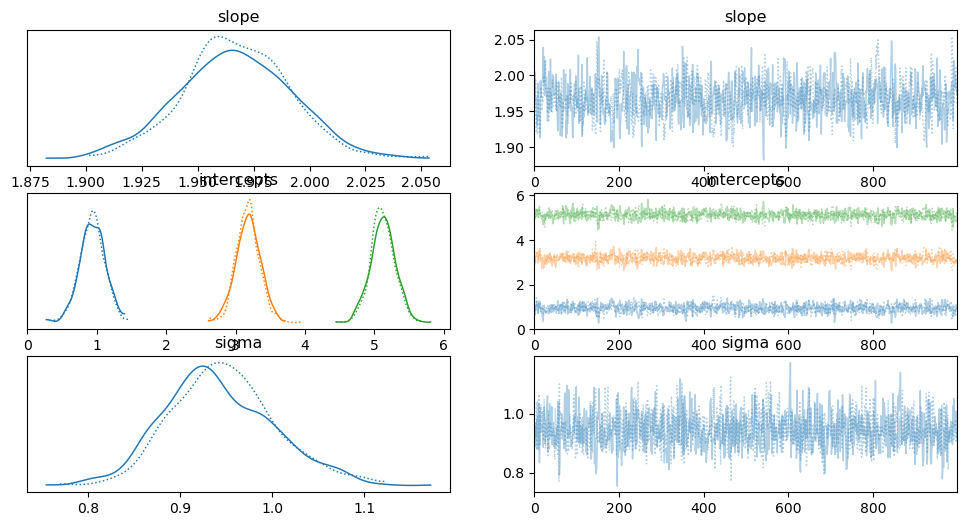
# Summarize the results
summary = pm.summary(trace)
print(summary)

# Plot the trace and posterior distributions for slope and intercepts
pm.traceplot(trace, var_names=['slope', 'intercepts', 'sigma'])
plt.show()

Step 6: Plot the Final Fitting

Now, let’s visualize the Bayesian fitting results by plotting the final regression lines for each group. We will use the mean posterior estimates for the slope and intercepts to generate the fitted lines.

# Extract the mean posterior estimates for the slope and intercepts
mean_slope = np.mean(trace['slope'])
mean_intercepts = np.mean(trace['intercepts'], axis=0)

# Plot the data points
plt.figure(figsize=(10, 6))
sns.scatterplot(x=X, y=Y, hue=group_labels, palette='viridis', alpha=0.6)

# Plot the fitted lines for each group
x_vals = np.linspace(0, 10, 100)
for idx, intercept in enumerate(mean_intercepts):
    y_vals = mean_slope * x_vals + intercept
    plt.plot(x_vals, y_vals, label=f'Fitted Line Group {idx+1}', linewidth=2)

# Add labels and legend
plt.xlabel('X')
plt.ylabel('Y')
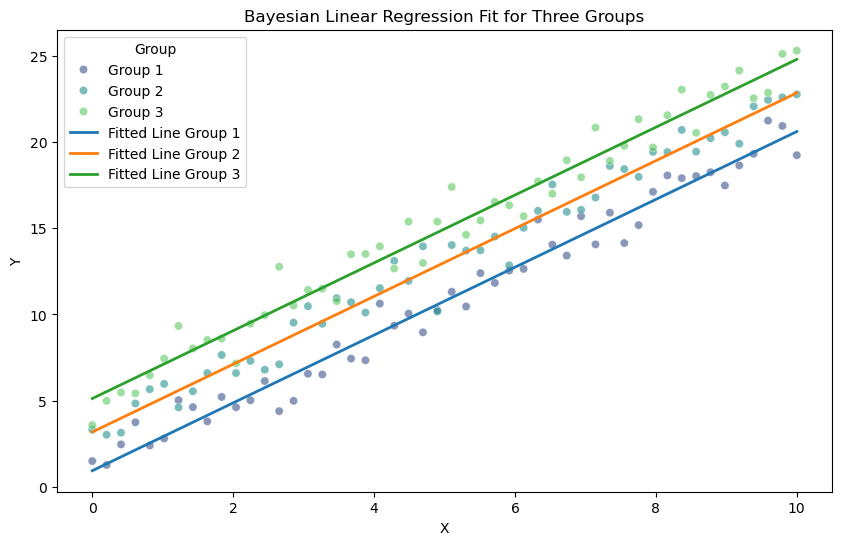
plt.title('Bayesian Linear Regression Fit for Three Groups')
plt.legend(title='Group')
plt.show()

Step 7: Posterior Distribution Analysis

To better understand the uncertainty in the model, we can plot the posterior distributions of the slope and intercepts using density plots. This will help visualize the spread of the estimates and their credible intervals.

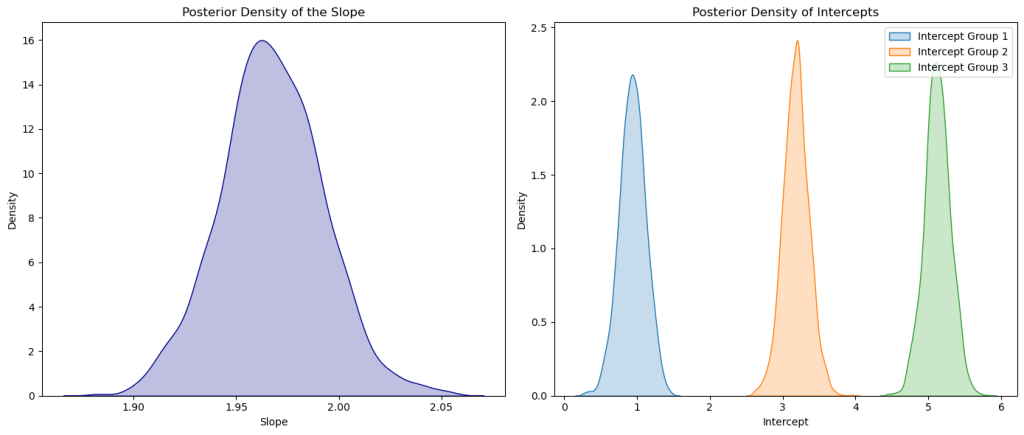
# Plot the posterior density for the slope
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
sns.kdeplot(trace['slope'], color='darkblue', shade=True)
plt.title('Posterior Density of the Slope')
plt.xlabel('Slope')
plt.ylabel('Density')

# Plot the posterior densities for the intercepts of each group
plt.subplot(1, 2, 2)
for i in range(3):
    sns.kdeplot(trace['intercepts'][:, i], label=f'Intercept Group {i+1}', shade=True)
plt.title('Posterior Density of Intercepts')
plt.xlabel('Intercept')
plt.ylabel('Density')
plt.legend()

plt.tight_layout()
plt.show()

Conclusions

In this tutorial, we performed Bayesian fitting for data from three groups where the regression lines were parallel, meaning they shared the same slope but had different intercepts.

Deja un comentario